You are looking for information, articles, knowledge about the topic nail salons open on sunday near me 쌍곡선 함수 적분 on Google, you do not find the information you need! Here are the best content compiled and compiled by the https://toplist.tfvp.org team, along with other related topics such as: 쌍곡선 함수 적분 역쌍곡선함수 적분, 쌍곡선함수 미분, Cosh 공식, Tanh 적분, 쌍곡함수, 삼각함수 적분, Sechx 적분, 쌍곡선함수 공식
[su_youtube_advanced url=”https://www.youtube.com/watch?v=BQZwzNbzmNg”]
역쌍곡선함수의 도함수/부정적분 : 네이버 블로그
- Article author: m.blog.naver.com
- Reviews from users: 20072
Ratings
- Top rated: 3.9
- Lowest rated: 1
- Summary of article content: Articles about 역쌍곡선함수의 도함수/부정적분 : 네이버 블로그 미적분(Old, 오류 많음). 역쌍곡선함수의 도함수/부정적분. 프로필. 네냐플. 2010. 9. 18. 8:00. 이웃추가. 본문 기타 기능. 본문 폰트 크기 조정 …
- Most searched keywords: Whether you are looking for 역쌍곡선함수의 도함수/부정적분 : 네이버 블로그 미적분(Old, 오류 많음). 역쌍곡선함수의 도함수/부정적분. 프로필. 네냐플. 2010. 9. 18. 8:00. 이웃추가. 본문 기타 기능. 본문 폰트 크기 조정
- Table of Contents:
카테고리 이동
네냐플(Nenyaffle)
이 블로그
미적분(Old 오류 많음)
카테고리 글
카테고리
이 블로그
미적분(Old 오류 많음)
카테고리 글

조금은 느리게 살자: 쌍곡선 함수(Hyperbolic Function)
- Article author: ghebook.blogspot.com
- Reviews from users: 8103
Ratings
- Top rated: 4.6
- Lowest rated: 1
- Summary of article content: Articles about
조금은 느리게 살자: 쌍곡선 함수(Hyperbolic Function)
여기서 C 는 적분 상수이다. [증명] 식 (2.4)에 있는 역함수의 미분을 사용해도 되지만, 다음처럼 변수 치환을 이용해도 쉽게 … … - Most searched keywords: Whether you are looking for
조금은 느리게 살자: 쌍곡선 함수(Hyperbolic Function)
여기서 C 는 적분 상수이다. [증명] 식 (2.4)에 있는 역함수의 미분을 사용해도 되지만, 다음처럼 변수 치환을 이용해도 쉽게 … - Table of Contents:
2020년 6월 24일 수요일
[아름다운 총서] 푸엥카레 가라사대 자연이 아름답지 않으면 연구는 필요 없다 연구가 없으면 삶도 없다
블로그 검색
번역기(Translator)
프로필
글목록
가장 많이 본 글
최근 댓글
관심 사용자
페이지뷰
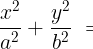
4. 쌍곡시컨트(sech x)의 적분법 | Integration of sech x
- Article author: cma-edu.tistory.com
- Reviews from users: 36430
Ratings
- Top rated: 3.2
- Lowest rated: 1
- Summary of article content: Articles about 4. 쌍곡시컨트(sech x)의 적분법 | Integration of sech x 첫 번째 시도로 시컨트의 적분에서처럼 자연로그를 시도할 수 있다. 그러나 삼각함수와 쌍곡선함수의 도함수에서 마이너스 차이로 인해 가능하지 … …
- Most searched keywords: Whether you are looking for 4. 쌍곡시컨트(sech x)의 적분법 | Integration of sech x 첫 번째 시도로 시컨트의 적분에서처럼 자연로그를 시도할 수 있다. 그러나 삼각함수와 쌍곡선함수의 도함수에서 마이너스 차이로 인해 가능하지 … 수학 모음 (Maths collection) 전체보기 0. $\int{\rm sech}\,x\,\textrm{d}x=\ln\vert{\rm sech}\,x+\tanh x\vert+c\,$? 첫 번째 시도로 시컨트의 적분에서처럼 자연로그를 시도할 수 있다. 그러나 삼각함수와 쌍..
- Table of Contents:
Cambridge Maths Academy
4 쌍곡시컨트(sech x)의 적분법 Integration of sech x 본문
수학 모음 (Maths collection) 전체보기
티스토리툴바

$\int \sqrt{1+x^2}dx$ 와 쌍곡함수(Hyperbolic Function)::::수학과 사는 이야기
- Article author: suhak.tistory.com
- Reviews from users: 6374
Ratings
- Top rated: 4.8
- Lowest rated: 1
- Summary of article content: Articles about $\int \sqrt{1+x^2}dx$ 와 쌍곡함수(Hyperbolic Function)::::수학과 사는 이야기 치환적분은 여러 가지 어려운 문제를 해결해 준다. 그 가운데 삼각치환은 멋지다. 삼각치환을 넘어 쌍곡치환까지 정리해 둔다. …
- Most searched keywords: Whether you are looking for $\int \sqrt{1+x^2}dx$ 와 쌍곡함수(Hyperbolic Function)::::수학과 사는 이야기 치환적분은 여러 가지 어려운 문제를 해결해 준다. 그 가운데 삼각치환은 멋지다. 삼각치환을 넘어 쌍곡치환까지 정리해 둔다. 치환적분은 여러 가지 어려운 문제를 해결해 준다. 그 가운데 삼각치환은 멋지다. 삼각치환을 넘어 쌍곡치환까지 정리해 둔다. $$\int \sqrt{1+x^2}dx$$ 간단한 꼴이지만 풀려고 나서면 쉽지는 않다. 먼저 삼각치..고등학교 수학, 미적분학, calculus, 면접, HTML, CSS, tistoryskin, Mathmatics, 여행, 사진, 야생화, 수학, 스킨
- Table of Contents:
$int sqrt{1+x^2}dx$ 와 쌍곡함수(Hyperbolic Function)
티스토리툴바

See more articles in the same category here: 17+ tips for you.
4. 쌍곡시컨트(sech x)의 적분법
반응형
0. $\int{\rm sech}\,x\,\textrm{d}x=\ln\vert{\rm sech}\,x+\tanh x\vert+c\,$?
첫 번째 시도로 시컨트의 적분에서처럼 자연로그를 시도할 수 있다. 그러나 삼각함수와 쌍곡선함수의 도함수에서 마이너스 차이로 인해 가능하지 않다는 것을 알게 된다. 이 차이점을 아는 것도 중요하므로 이 부분부터 살펴보자.
우리에게 필요한 도함수들은 다음과 같다.
$$ \begin{align} \frac{\textrm{d}}{\textrm{d}x}\tan x&=\sec^2x & \frac{\textrm{d}}{\textrm{d}x}\tanh x&={\rm sech}^2x \\ \frac{\textrm{d}}{\textrm{d}x}\sec x&=\sec x\tan x & \frac{\textrm{d}}{\textrm{d}x}{\rm sech}\,x&=-{\rm sech}\,x\tanh x \end{align} $$
여기서 ${\rm sech}\,x\,$에 있는 마이너스 사인으로 인해 자연로그 형태가 나오지 않게 됨을 확인할 수 있다.
$$ \begin{align} \frac{\textrm{d}}{\textrm{d}x}(\sec x+\tan x)&=\sec x\tan x+\sec^2x=\sec x(\sec x+\tan x) \\ \frac{\textrm{d}}{\textrm{d}x}({\rm sech}\,x+\tanh x)&=-{\rm sech}\,x\tanh x+{\rm sech}^2x={\rm sech}\,x({\rm sech}\,x-\tanh x) \\ \int{\rm sech}\,x\,\textrm{d}x&=\int\frac{{\rm sech}\,x({\rm sech}\,x+\tanh x)}{{\rm sech}\,x+\tanh x}\,\textrm{d}x
e\ln\vert{\rm sech}\,x+\tanh x\vert+c \end{align} $$
1. $u=\textrm{e}^x$ 치환적분
$$ \int{\rm sech}\,x\,\textrm{d}x=2\arctan\left(\textrm{e}^x\right)+c $$
책에 가장 많이 등장하는 표준적인 방법은 쌍곡선함수(hyperbolic function)을 지수함수 정의로 나타내어 치환하는 방법이다.
$$ \begin{align} \cosh x&=\frac{\textrm{e}^x+\textrm{e}^{-x}}{2},& \sinh x&=\frac{\textrm{e}^x-\textrm{e}^{-x}}{2} \\ {\rm sech}\,x&=\frac{2}{\textrm{e}^x+\textrm{e}^{-x}}=\frac{2\textrm{e}^x}{\textrm{e}^{2x}+1} \end{align} $$
이제 $u=\textrm{e}^x$ 치환을 사용하여 적분을 전개하면 ($\textrm{d}u=\textrm{e}^x\,\textrm{d}x=u\,\textrm{d}x$),
$$ \begin{align} \int{\rm sech}\,x\,\textrm{d}x&=\int\frac{2\textrm{e}^x}{\textrm{e}^{2x}+1}\,\textrm{d}x \\ &=\int\frac{2}{u^2+1}\,\textrm{d}u \qquad (u=\tan z,\quad \textrm{d}u=\sec^2z\,\textrm{d}z) \\ &=\int\frac{2}{\tan^2z+1}\cdot\sec^2z\,\textrm{d}z \\ &=\int2\,\textrm{d}z \\ &=2z+c \\ &=2\arctan u+c \\ &=2\arctan\left(\textrm{e}^x\right)+c \qquad \square \end{align} $$
2. $u=\sinh x$ 치환과 부분분수(partial fractions)
$$ \int{\rm sech}\,x\,\textrm{d}x=\arctan(\sinh x)+c $$
시컨트/세칸트의 적분에서 본 아이작 배로우(Isaac Barrow, 1630-1677)의 방법을 쌍곡선함수/하이퍼볼릭 함수에도 그대로 적용할 수 있다. 다만, 부분분수가 아니라 적분의 결과가 탄젠트의 역함수(inverse tangent, arctan)로 나타난다.
$$ \begin{align} \int{\rm sech}\,x&=\int\frac1{\cosh x}\,\textrm{d}x \\ &=\int\frac{\cosh x}{\cosh^2x}\,\textrm{d}x \\ &=\int\frac{\cosh x}{1+\sinh^2x}\,\textrm{d}x \qquad (u=\sinh x,\quad \textrm{d}u=\cosh x\,\textrm{d}x) \\ &=\int\frac{\textrm{d}u}{1+u^2} \\ &=\int\frac{\sec^2z}{1+\tan^2z}\,\textrm{d}z \qquad (u=\tan z,\quad \textrm{d}u=\sec^2z\,\textrm{d}z) \\ &=\int \textrm{d}z \\ &=z+c \\ &=\arctan u+c \\ &=\arctan(\sinh x)+c \qquad \square \end{align} $$
Comment: 방법1과 동일함은 잠시 후 부록에서 확인하도록 하자.
3. $t=\tanh\frac{x}2$ 치환 (t-치환 또는 바이어슈트라스 치환)
$$ \int{\rm sech}\,x\,\textrm{d}x=2\arctan\left(\tanh\frac{x}2\right)+c $$
시컨트와 코시컨트 적분과 마찬가지로 t-치환 또는 바이어슈트라스 치환(Weierstrass substitution)을 사용할 수 있다. 삼각함수와 마찬가지로 t-치환의 핵심은 $t=\tanh\frac{x}2\,$을 사용하여 $\textrm{d}x$, $\cosh x\,$와 $\sinh x\,$를 모두 t를 사용한 분수(유리함수)로 나타낼 수 있다는 데 있다.
$$ \begin{align} \textrm{d}t&=\frac12\underbrace{{\rm sech}^2\frac{x}2}_{1-\tanh^2\frac{x}2}\,\textrm{d}x=\frac{1-\tanh^2\frac{x}2}2\,\textrm{d}x=\frac{1-t^2}2\,\textrm{d}x \\ \textrm{d}x&=\frac{2}{1-t^2}\,\textrm{d}t \\ \\ \cosh x&=\cosh^2\frac{x}2+\sinh^2\frac{x}2=\cosh^2\frac{x}2\left(1+\tanh^2\frac{x}2\right)=\frac{1+\tanh^2\frac{x}2}{{\rm sech}^2\frac{x}2}=\frac{1+\tanh^2\frac{x}2}{1-\tanh^2\frac{x}2}=\frac{1+t^2}{1-t^2} \\ \sinh x&=2\sinh\frac{x}2\cosh\frac{x}2=2\cosh^2\frac{x}2\tanh^2\frac{x}2=\frac{2\tanh^2\frac{x}2}{{\rm sech}^2\frac{x}2}=\frac{2\tanh^2\frac{x}2}{1-\tanh^2\frac{x}2}=\frac{2t}{1-t^2} \end{align} $$
이제 쌍곡시컨트/쌍곡세칸트 적분에 적용하면,
$$ \begin{align} \int{\rm sech}\,x\,\textrm{d}x &=\int\frac1{\cosh x}\,\textrm{d}x \\ &=\int\frac1{\frac{1+t^2}{1-t^2}}\frac{2}{1-t^2}\,\textrm{d}t \\ &=\int\frac2{1+t^2}\,\textrm{d}t \qquad (t=\tan z,\quad \textrm{d}t=\sec^2z\,\textrm{d}z)\\ &=\int\frac{2\sec^2z}{1+\tan^2z}\,\textrm{d}z \\ &=\int2\,\textrm{d}z \\ &= 2z+c \\ &=2\arctan t+c \\ &=2\arctan\left(\tanh\frac{x}2\right)+c \qquad \square \end{align} $$
Comment: 방법 1, 방법 2와의 동일함은 부록에서 확인할 수 있다.
부록 1: 세 결과의 동일함
앞서 예고한 것처럼 달리 보이는 세 결과의 동일함을 증명해보자. 세 결과를 다시 적어보면 다음과 같다. (계산을 단순히 하기 위해 적분상수는 잠시 무시하자.)
$$ \begin{align} \theta&=2\arctan\left(\textrm{e}^x\right) \\ \phi&=\arctan(\sinh x)=\arctan\left(\frac{\textrm{e}^x-\textrm{e}^{-x}}{2}\right)=\arctan\left(\frac{\textrm{e}^{2x}-1}{2\textrm{e}^x}\right) \\ \psi&=2\arctan\left(\tanh\frac{x}2\right)=2\arctan\left(\frac{\textrm{e}^x-1}{\textrm{e}^x+1}\right) \end{align} $$
(1) $\phi=\psi$ (방법2 = 방법3)
2배각 공식(double angle formulae)을 이용하여 $\theta\,$와 $\psi\,$를 나타낼 수 있다.
$$ \begin{align} \tan\frac{\theta}{2}&=\textrm{e}^x &&\Rightarrow& \tan\theta&=\frac{2\tan\frac{\theta}2}{1-\tan^2\frac{\theta}2}=\frac{2\textrm{e}^x}{1-\textrm{e}^{2x}} \\ \tan\frac{\psi}2&=\frac{\textrm{e}^x-1}{\textrm{e}^x+1} &&\Rightarrow& \tan\psi&=\frac{2\tan\frac{\psi}2}{1-\tan^2\frac{\psi}2}=\frac{2\cdot\frac{\textrm{e}^x-1}{\textrm{e}^x+1}}{\underbrace{\left(1-\frac{\textrm{e}^x-1}{\textrm{e}^x+1}\right)}_{\frac2{\textrm{e}^x+1}}\underbrace{\left(1+\frac{\textrm{e}^x-1}{\textrm{e}^x+1}\right)}_{\frac{2\textrm{e}^x}{\textrm{e}^x+1}}}=\frac{\textrm{e}^{2x}-1}{2\textrm{e}^x} \\ &&&\Rightarrow& \psi&=\arctan\left(\frac{\textrm{e}^{2x}-1}{2\textrm{e}^x}\right)=\phi \qquad \square \end{align} $$
따라서 $\phi\,$와 $\psi\,$는 같은 표현임을 알 수 있다.
(2) $\theta=\phi$ (방법1 = 방법2)
반면 $\theta\,$는 $\phi\,$와 역수의 관계를 가지고, 음수 부호가 다르다는 것을 알 수 있다. 이제 적분상수가 들어올 차례다. 즉, $-\cot\theta\,$와 $\tan\phi\,$가 동일하므로, 적분상수를 적절히 변환하면 같은 표현을 얻을 수 있다. 여기서 약간의 추측(guesswork)이 필요한데, $\theta\,$의 적분상수로 $-\frac{\pi}2$를 더해 다음과 같이 표현해보자.
$$ \begin{align} \theta&=2\arctan\left(\textrm{e}^x\right)-\frac{\pi}2 \\ \theta+\frac{\pi}2&=2\arctan\left(\textrm{e}^x\right) \\ \tan\left(\frac{\theta}2+\frac{\pi}4\right)&=\frac{1+\tan\frac{\theta}2}{1-\tan\frac{\theta}2}=\textrm{e}^x \\ \Rightarrow\quad \tan\frac{\theta}2&=\frac{\textrm{e}^x-1}{\textrm{e}^x+1} \\ \Rightarrow\quad \tan\theta&=\frac{2\tan\frac{\theta}2}{1-\tan^2\frac{\theta}2}=\frac{2\cdot\frac{\textrm{e}^x-1}{\textrm{e}^x+1}}{\underbrace{\left(1-\frac{\textrm{e}^x-1}{\textrm{e}^x+1}\right)}_{\frac2{\textrm{e}^x+1}}\underbrace{\left(1+\frac{\textrm{e}^x-1}{\textrm{e}^x+1}\right)}_{\frac{2\textrm{e}^x}{\textrm{e}^x+1}}}=\frac{\textrm{e}^{2x}-1}{2\textrm{e}^x}=\phi \qquad \square \end{align} $$
Comment: 여기서 추측(guesswork)이라고 했는데, 추측 과정을 적어보면 다음과 같다. 우선 $\theta\,$에 적분상수 $-c$를 더한다고 해보자.
$$ \begin{align} \theta&=2\arctan\left(\textrm{e}^x\right)-c \\ \frac{\theta+c}2&=\arctan\left(\textrm{e}^x\right) \\ \tan\left(\frac{\theta+c}{2}\right)&=\textrm{e}^x \end{align} $$
이제 남은 건 c값을 찾아내는 일이다. 앞선 계산을 통해 $\tan\phi=-\cot\theta\,$의 관계를 알아냈다. 아직 $\phi\,$와 $\theta\,$의 정확한 관계는 모르기 때문에 $\tan\phi=-\cot\alpha\,$라고 가정하고 $\alpha\,$와 $\theta\,$를 관계지어보자.
$$ \begin{align} \tan\phi=-\cot\alpha&=\frac{\textrm{e}^{2x}-1}{2\textrm{e}^x} \\ \Rightarrow\quad \tan\alpha&=\frac{2\textrm{e}^x}{1-\textrm{e}^{2x}}=\frac{2\tan\frac{\alpha}2}{1-\tan^2\frac{\alpha}2} \\ \Rightarrow\quad \tan\frac{\alpha}2&=\textrm{e}^x\end{align} $$
이제 다음 관계들 중
$$ \begin{align} \tan\left(x\pm\frac{\pi}2\right)&=-\cot x \\ \tan\left(x\pm\frac{3\pi}2\right)&=-\cot x \\ \tan\left(x-\frac{\pi}2+n\pi\right)&=-\cot x,\quad n\in\mathbb Z \end{align} $$
가장 일반적인 세 번째 관계를 이용하여 $\theta\,$와 $\alpha\,$를 연결지을 수 있다.
$$ \begin{align} \textrm{e}^x=\tan\frac{\alpha}2&=\tan\left(\frac{\theta+c}2\right) \\ \Rightarrow\quad \frac{\alpha}2&=\frac{\theta+c}2+n\pi,\quad n\in\mathbb Z \\ \Rightarrow\quad \alpha&=\theta+c+2n\pi,\quad n\in\mathbb Z \end{align} $$
이제 $\tan\alpha=-\cos\phi\,$라는 점을 이용하여, 즉 탄젠트 함수와 $\alpha\,$를 통해 $\theta\,$와 $\phi\,$를 연결지으면
$$ \tan\alpha=\tan(\theta+c)=-\cot\phi=\tan\left(\phi-\frac{\pi}2+n\pi\right),\quad n\in\mathbb Z $$
그리고 c값을 적절히 선택하면 $\theta=\phi\,$를 등치시킬 수 있다.
$$ c=n\pi-\frac{\pi}2=\left(n-\frac12\right)\pi,\quad n\in\mathbb Z $$
앞서 우리는 이 중 가장 간단한 $n=1$, 즉 $c=\frac{\pi}2\,$를 선택한 것이었다.
Cross-check: 계산 확인을 위해 $c=-\frac{\pi}2\,$의 경우에도 $\theta=\phi\,$를 얻는지 살펴보자.
$$ \begin{align} \theta&=2\arctan\left(\textrm{e}^x\right)+\frac{\pi}2 \\ \theta-\frac{\pi}2&=2\arctan\left(\textrm{e}^x\right) \\ \tan\left(\frac{\theta}2-\frac{\pi}4\right)&=\frac{\tan\frac{\theta}2-1}{1+\tan\frac{\theta}2}=\textrm{e}^x \\ \Rightarrow\quad \tan\frac{\theta}2&=\frac{1+\textrm{e}^x}{1-\textrm{e}^x} \\ \Rightarrow\quad \tan\theta&=\frac{2\tan\frac{\theta}2}{1-\tan^2\frac{\theta}2}=\frac{2\cdot\frac{1+\textrm{e}^x}{1-\textrm{e}^x}}{\underbrace{\left(1-\frac{1+\textrm{e}^x}{1-\textrm{e}^x}\right)}_{\frac{-2\textrm{e}^x}{1-\textrm{e}^x}}\underbrace{\left(1+\frac{1+\textrm{e}^x}{1-\textrm{e}^x}\right)}_{\frac{2}{1-\textrm{e}^x}}}=\frac{\textrm{e}^{2x}-1}{2\textrm{e}^x}=\phi \qquad \square \end{align} $$
이제 세 결과를 한 줄로 요약하면 (이제 적분상수 c는 모두 같은 값이라고 생각할 수 있다),
$$ \begin{align} \int{\rm sech}\,x\,\textrm{d}x&=2\arctan\left(\textrm{e}^x\right)+\left(n-\frac12\right)\pi+c \\ &=\arctan(\sinh x)+c \\ &=2\arctan\left(\tanh\frac{\pi}2\right)+c \end{align} $$
부록2: t-치환 / 바이어슈트라스 치환 $t=\tanh\frac{x}2$
t-치환으로 쌍곡시컨트(sech)와 쌍곡코시컨트(csch) 적분을 할 수 있지만, 이 두 적분만 하고 멈추기에 t-치환은 너무도 효율적인 도구다.
앞서 유도한 결과를 다시 요약해보자.
$$ \textrm{d}x=\frac{2}{1-t^2}\,\textrm{d}t, \qquad \cosh x=\frac{1+t^2}{1-t^2}, \qquad \sin x=\frac{2t}{1-t^2} $$
또한 다른 삼각함수($\tan$, $\sec$, $\csc$, $\cot$)도 t를 사용해 나타낼 수 있다.
$$ \tanh x=\frac{2t}{1+t^2},\quad {\rm sech}\,x=\frac{1-t^2}{1+t^2}, \quad {\rm csch}\,x=\frac{1-t^2}{2t}, \quad \coth x=\frac{1+t^2}{2t} $$
이를 이용하면 $\cosh x$, $\sinh x$이 들어있는 모든 적분을 다음과 같이 쓸 수 있다.
$$ \int \textrm{f}(\cosh x,\sinh x)\,\textrm{d}x = \int \textrm{f}\left(\frac{1+t^2}{1-t^2},\frac{2t}{1-t^2}\right)\frac{2}{1-t^2}\,\textrm{d}t $$
이중 가장 대표적인 예는
$$\int\frac1{a\cosh x+b\sinh x+c}\,\textrm{d}x$$
로서 보다 자세한 내용은 t-치환/바이어슈트라스 치환(t-substitution, Weierstrass substitution)참조.
반응형
쌍곡선함수와 역쌍곡선함수의 미분 – SASA Math
이 포스트에서는 쌍곡선함수와 역쌍곡선함수를 정의하고 이 함수들의 도함수를 살펴본다.
쌍곡선함수의 정의
\(\mathbb{R}\)에서 정의된 함수는 기함수와 우함수의 합으로 나타낼 수 있다. 즉 함수 \(f\)는 \[f(x) = \frac{f(x)-f(-x)}{2} + \frac{f(x)+f(-x)}{2}\] 로서 기함수와 우함수의 합으로 표현된다. 이와 같은 방법으로 자연지수함수를 기함수와 우함수의 합으로 표현하면 \[e^x = \frac{e^x – e^{-x}}{2} + \frac{e^x + e^{-x}}{2}\] 이다. 이때 \(e^x\)의 기함수 부분을 쌍곡선사인, 우함수 부분을 쌍곡선코사인이라고 부른다. 즉 쌍곡선사인(hyperbolic sine)이란 \[\sinh x = \frac{e^x – e^{-x}}{2}\] 으로 정의된 함수 \(\sinh\)를 이르며, 쌍곡선코사인(hyperbolic cosine)이란 \[\cosh x = \frac{e^x + e^{-x}}{2}\] 으로 정의된 함수 \(\cosh\)를 이른다. 사인과 코사인을 이용하여 다른 네 개의 삼각함수를 모두 표현할 수 있는 것처럼 쌍곡선사인과 쌍곡선코사인을 이용하여 다른 네 개의 쌍곡선함수를 모두 표현할 수 있다. 즉 다음과 같이 정의한다. \[
ewcommand{sech}[]{\operatorname{sech}}
ewcommand{csch}[]{\operatorname{csch}} \begin{align} \tanh x &= \frac{\sinh x}{\cosh x} = \frac{e^x – e^{-x}}{e^x + e^{-x}} ,\\[6pt] \coth x &= \frac{\cosh x}{\sinh x} = \frac{e^x + e^{-x}}{e^x – e^{-x}} ,\\[6pt] \sech x &= \frac{1}{\cosh x} = \frac{2}{e^x + e^{-x}} ,\\[6pt] \csch x &= \frac{1}{\sinh x} = \frac{2}{e^x – e^{-x}} . \end{align} \] 위 네 개의 함수를 순서대로 쌍곡선탄젠트, 쌍곡선코탄젠트, 쌍곡선시컨트, 쌍곡선코시컨트라고 부른다. 그리고 지금까지 소개한 여섯 개의 함수를 통틀어 쌍곡선함수(hyperbolic function)라고 부른다.
쌍곡선함수에 삼각함수의 이름이 붙은 이유는 사인과 코사인이 기함수와 우함수의 대표적인 함수이기도 하거니와, 쌍곡선함수가 삼각함수와 비슷한 성질을 가지고 있기 때문이다.
쌍곡선함수와 관련된 항등식 \[\begin{align} \cosh^2 x &- \sinh^2 x = 1 ,\\[8pt] \sinh 2x &= 2 \sinh x \cosh x ,\\[8pt] \cosh 2x &= \cosh^2 x + \sinh^2 x ,\\[6pt] \cosh^2 x &= \frac{\cosh 2x +1}{2} ,\\[4pt] \sinh^2 x &= \frac{\cosh 2x -1}{2} ,\\[6pt] \tanh^2 x &= 1- \sech^2 x ,\\[8pt] \coth^2 x &= 1+ \csch^2 x . \end{align}\] \[\begin{align} \cosh^2 x &- \sinh^2 x = 1 ,\\[8pt] \sinh 2x &= 2 \sinh x \cosh x ,\\[8pt] \cosh 2x &= \cosh^2 x + \sinh^2 x ,\\[6pt] \cosh^2 x &= \frac{\cosh 2x +1}{2} ,\\[4pt] \sinh^2 x &= \frac{\cosh 2x -1}{2} ,\\[6pt] \tanh^2 x &= 1- \sech^2 x ,\\[8pt] \coth^2 x &= 1+ \csch^2 x . \end{align}\]
여기서 첫 번째 등식을 유심히 살펴볼 필요가 있다. 좌표평면에서 \((\cosh t ,\, \sinh t )\)로 표현되는 점의 좌표는 \(x^2 – y^2 = 1\)을 만족시키므로, 이 점은 쌍곡선 위에 놓이게 된다. 쌍곡선함수의 이름에 ‘쌍곡선’이라는 접두사가 붙는 것은 바로 이 때문이다.
쌍곡선함수의 미분
쌍곡선함수는 자연지수함수를 이용하여 정의되기 때문에, 쌍곡선함수의 도함수를 구하는 것은 쉽다. \[\begin{align} \frac{d}{dx} \sinh x &= \frac{d}{dx} \frac{e^x – e^{-x}}{2} \\[4pt]&= \frac{e^x + e^{-x}}{2} = \cosh x,\\[10pt] \frac{d}{dx} \cosh x &= \frac{d}{dx} \frac{e^x + e^{-x}}{2} \\[4pt]&= \frac{e^x – e^{-x}}{2} = \sinh x,\\[10pt] \frac{d}{dx} \tanh x &= \frac{d}{dx} \frac{\sinh x}{\cosh x} = \frac{\cosh^2 x – \sinh^2}{(\cosh x)^2} \\[4pt]&= \frac{1}{(\cosh x)^2} = \sech^2 x ,\\[10pt] \frac{d}{dx} \coth x &= \frac{d}{dx} \frac{\cosh x}{\sinh x} = \frac{\sinh^2 x – \cosh^2}{(\sinh x)^2} \\[4pt]&= \frac{-1}{(\sinh x)^2} = -\csch^2 x \,\,\, (x
e 0),\\[10pt] \frac{d}{dx} \sech x &= \frac{d}{dx} \frac{1}{\cosh x} = \frac{-\sinh x}{(\cosh x)^2} \\[4pt]&= – \sech x \tanh x ,\\[10pt] \frac{d}{dx} \csch x &= \frac{d}{dx} \frac{1}{\sinh x} = \frac{-\cosh x}{(\sinh x)^2} \\[4pt]&= – \csch x \coth x \,\,\, (x
e 0). \end{align}\] 이것을 정리하면 다음과 같다.
정리 1. (쌍곡선함수의 도함수) \[\begin{align} \frac{d}{dx} \sinh x &= \cosh x,\\[6pt] \frac{d}{dx} \cosh x &= \sinh x,\\[6pt] \frac{d}{dx} \tanh x &= \sech^2 x ,\\[6pt] \frac{d}{dx} \coth x &= -\csch^2 x &(&x
e 0),\\[6pt] \frac{d}{dx} \sech x &= – \sech x \tanh x ,\\[6pt] \frac{d}{dx} \csch x &= – \csch x \coth x &(&x
e 0). \end{align}\] \[\begin{align} \frac{d}{dx} \sinh x &= \cosh x,\\[6pt] \frac{d}{dx} \cosh x &= \sinh x,\\[6pt] \frac{d}{dx} \tanh x &= \sech^2 x ,\\[6pt] \frac{d}{dx} \coth x &= -\csch^2 x &(&x
e 0),\\[6pt] \frac{d}{dx} \sech x &= – \sech x \tanh x ,\\[6pt] \frac{d}{dx} \csch x &= – \csch x \coth x &(&x
e 0). \end{align}\]
역쌍곡선함수의 미분
쌍곡선사인, 쌍곡선탄젠트, 쌍곡선코탄젠트, 쌍곡선코시컨트는 일대일 함수이므로 그 역함수를 정의할 수 있다. 그러나 쌍곡선코사인과 쌍곡선시컨트는 일대일 함수가 아니므로 그 역함수를 정의할 수 없다. 하지만 삼각함수의 정의역을 축소하여 일대일 함수가 되도록 하고 그 역함수를 정의한 것처럼 쌍곡선코사인과 쌍곡선시컨트의 정의역을 축소하고 그 역함수를 정의할 수 있다. 이러한 관점에서 역쌍곡선함수를 다음과 같이 정의한다. \[\begin{align} y = \sinh^{-1} x \,\, &\Longleftrightarrow \,\, x = \sinh y \,\,\,\text{for}\,\,\,y\in\mathbb{R} ,\\[8pt] y = \cosh^{-1} x \,\, &\Longleftrightarrow \,\, x = \cosh y \,\,\,\text{for}\,\,\,y\in [0,\,\infty ) ,\\[8pt] y = \tanh^{-1} x \,\, &\Longleftrightarrow \,\, x = \tanh y \,\,\,\text{for}\,\,\,y\in\mathbb{R} ,\\[8pt] y = \coth^{-1} x \,\, &\Longleftrightarrow \,\, x = \coth y \,\,\,\text{for}\,\,\,y\in\mathbb{R} \setminus \left\{ 0 \right\},\\[8pt] y = \sech^{-1} x \,\, &\Longleftrightarrow \,\, x = \sech y \,\,\,\text{for}\,\,\,y\in [0,\,\infty ) ,\\[8pt] y = \csch^{-1} x \,\, &\Longleftrightarrow \,\, x = \csch y \,\,\,\text{for}\,\,\,y\in\mathbb{R} \setminus \left\{ 0 \right\}. \end{align}\] 정의에 의하여 역쌍곡선함수는 다음과 같은 정의역을 가진다. \[\begin{align} y = \sinh^{-1} x \,\,\,&\text{for}\,\,\,x\in\mathbb{R} ,\\[8pt] y = \cosh^{-1} x \,\,\,&\text{for}\,\,\,x\in [1,\,\infty ) ,\\[8pt] y = \tanh^{-1} x \,\,\,&\text{for}\,\,\,x\in (-1,\,1) ,\\[8pt] y = \coth^{-1} x \,\,\,&\text{for}\,\,\,x\in\mathbb{R} \setminus [-1,\,1],\\[8pt] y = \sech^{-1} x \,\,\,&\text{for}\,\,\,x\in (0,\,1] ,\\[8pt] y = \csch^{-1} x \,\,\,&\text{for}\,\,\,x\in\mathbb{R} \setminus \left\{ 0 \right\}. \end{align}\] 쌍곡선함수의 정의에 의하여 \(0 < x \le 1\)일 때 \[\sech \left( \cosh^{-1} \left( \frac{1}{x} \right) \right) = \frac{1}{\cosh \left( \cosh^{-1} \left( \frac{1}{x} \right) \right)} = \frac{1}{\left(\frac{1}{x}\right)} = x\] 이다. 그런데 \(\sech (\sech^{-1} x ) =x\)이므로 \[\cosh^{-1} \left( \frac{1}{x} \right) = \sech^{-1} x\] 를 얻는다. 비슷한 방법으로 다음 등식을 얻는다. 역쌍곡선함수와 관련된 항등식 \[\begin{align} \sech^{-1} x &= \cosh^{-1} \frac{1}{x}, \\[6pt] \csch^{-1} x &= \sinh^{-1} \frac{1}{x}, \\[6pt] \coth^{-1} x &= \tanh^{-1} \frac{1}{x} . \end{align}\] \[\begin{align} \sech^{-1} x &= \cosh^{-1} \frac{1}{x}, \\[6pt] \csch^{-1} x &= \sinh^{-1} \frac{1}{x}, \\[6pt] \coth^{-1} x &= \tanh^{-1} \frac{1}{x} . \end{align}\] 이제 역쌍곡선함수의 도함수를 구해 보자. \[\begin{align} \frac{d}{dx} (\sinh^{-1} x ) &=\frac{1}{\cosh (\sinh^{-1} x)} \\[4pt] &=\frac{1}{\sqrt{1+\sinh^2 (\sinh^{-1} x)}} \\[4pt] &=\frac{1}{\sqrt{1+x^2}},\\[8pt] \frac{d}{dx} (\cosh^{-1} x ) &=\frac{1}{\sinh (\cosh^{-1} x)} \\[4pt] &=\frac{1}{\sqrt{\cosh^2 (\cosh^{-1} x)}-1} \\[4pt] &=\frac{1}{\sqrt{x^2 -1}} \quad (x > 1),\\[8pt] \frac{d}{dx} (\tanh^{-1} x) &=\frac{1}{\sech^2 (\tanh^{-1} x)} \\[4pt] &=\frac{1}{\sqrt{1-\tanh^2 (\tanh^{-1} x)}} \\[4pt] &=\frac{1}{\sqrt{1-x^2}} \quad (\lvert x \rvert < 1),\\[8pt] \frac{d}{dx} (\coth^{-1} x ) &=\frac{1}{-\csch^2 (\coth^{-1} x)} \\[4pt] &=\frac{1}{1-\coth^2 (\coth^{-1} x)} \\[4pt] &=\frac{1}{1-x^2} \quad (\lvert x \rvert > 1),\\[8pt] \frac{d}{dx} (\sech^{-1} x) &=\frac{d}{dx} \left( \cosh^{-1} \frac{1}{x} \right) \\[4pt] &=\frac{1}{\sqrt{\frac{1}{x^2}-1}} \cdot \left( -\frac{1}{x^2}\right) \\[4pt] &= – \frac{1}{x\sqrt{1-x^2}} \quad (0 < x < 1),\\[8pt] \frac{d}{dx} (\csch^{-1} x) &=\frac{d}{dx} \sinh^{-1} \frac{1}{x} \\[4pt] &=\frac{1}{\sqrt{1+\frac{1}{x^2}}} \cdot \left( -\frac{1}{x^2}\right) \\[4pt] &= - \frac{1}{\lvert x \rvert \sqrt{1+x^2}} \quad (x e 0). \end{align}\] 이것을 정리하면 다음과 같다.
$\int \sqrt{1+x^2}dx$ 와 쌍곡함수(Hyperbolic Function)
반응형
치환적분은 여러 가지 어려운 문제를 해결해 준다. 그 가운데 삼각치환은 멋지다. 삼각치환을 넘어 쌍곡치환까지 정리해 둔다.
$$\int \sqrt{1+x^2}dx$$
간단한 꼴이지만 풀려고 나서면 쉽지는 않다. 먼저 삼각치환을 써보자.
$$x=\tan\theta\quad\quad dx=\sec^2\theta d \theta$$
정리하면
$$\int \sqrt{1+\tan^2\theta}\sec^2\theta d \theta=\int \sec^3 \theta d\theta$$
결국 $I=\int \sec^3 \theta d\theta$의 부정적분을 찾아야 한다.
$$I=\int \sec \theta \cdot \sec^2 \theta d\theta=\int \sec\theta \frac{d(\tan \theta)}{d\theta}d \theta$$
부분적분을 쓰자.
$$=\sec\theta\tan\theta-\int \sec\theta\tan^2\theta d \theta=\sec\theta\tan\theta-\int \sec\theta(\sec^2\theta -1)d \theta$$
$$=\sec\theta\tan\theta-\int \sec^3\theta d \theta+\int\sec\theta d \theta$$
$$2I=\sec\theta\tan\theta+\int\frac{\sec\theta(\sec\theta+\tan\theta)}{\sec\theta+\tan\theta} d \theta$$
$$I=\frac{1}{2}\sec\theta\tan\theta+\frac{1}{2}\ln{|\sec\theta+\tan\theta|} +C$$
위에서 치환했던 변수를 되돌려 놓자.
$$\tan\theta=x,\quad\quad \sec\theta =\pm\sqrt{1+\tan^2 \theta}=\sqrt{1+x^2}$$
이므로 $\sec \theta>0$이라고 한다면
$$\int \sqrt{1+x^2}dx=\frac{1}{2}x\sqrt{1+x^2} +\frac{1}{2}\ln{|\sqrt{1+x^2}+x|} +C$$
이다. 생각보다 복잡하다.
참고로 $\int \sec^3 x dx$를 구하는 또 다른 방법도 있다.
$$\int \sec^3 x \, dx = \int \frac{dx}{\cos^3 x} = \int \frac{\cos x\,dx}{\cos^4 x} = \int \frac{\cos x\,dx}{(1-\sin^2 x)^2} = \int \frac{du}{(1-u^2)^2}$$
$$u = \sin x,\quad du = \cos x\,dx$$
$$ \frac{1}{(1-u^2)^2} = \frac{1/4}{1-u} + \frac{1/4}{(1-u)^2} + \frac{1/4}{1+u} + \frac{1/4}{(1+u)^2}$$
$$ =-\frac 1 4\ln (1-u) + \frac{1/4}{1-u} + \frac 1 4 \ln(1+u) – \frac{1/4}{1+u} + C $$
$$= \frac 1 4 \ln \frac{1+u}{1-u} + \frac 1 2 \frac{u}{1-u^2} + C $$
$$= \frac 1 4 \ln\frac{1+\sin x}{1-\sin x} + \frac 1 2 \frac{\sin x}{\cos^2 x} = \frac 1 4 \ln\frac{1+\sin x}{1-\sin x} + \frac 1 2 \sec x \tan x + C$$
다른 쉬운 방법은 없을까? 뜬금없어 보이지만 $$x=\frac{1}{2}(e^t -e^{-t})$$로 치환해 보자.
$$1+x^2 =1+ \frac{1}{4}(e^t -e^{-t})^2=\frac{1}{4}(e^t +e^{-t})^2,\quad dx=\frac{1}{2}(e^t +e^{-t})dt$$
이므로
$$\int \sqrt{1+x^2}dx=\int\frac{1}{4}(e^t +e^{-t})^2 dt=\frac{1}{4}\int(e^{2t} +e^{-2t}+2) dt$$
$$=\frac{1}{4}(\frac{1}{2}e^{2t}-\frac{1}{2}e^{-2t}+2t)+C=\frac{1}{8}(e^t -e^{-t})(e^t+e^{-t})+\frac{t}{2}+C$$
$2x=e^t -e^{-t}\quad e^{2t}-2x e^t -1=0$에서 $e^t =x+\sqrt{1+x^2}$이므로 $t=\ln|x+\sqrt{1+x^2}|$이다.
또한, $\displaystyle{x^2 +1= \frac{1}{4}(e^t +e^{-t})^2}$이므로 $\displaystyle{\frac{1}{2}(e^t+e^{-t})=\sqrt{1+x^2}}$이다.
다시 정리하면 삼각치환으로 했을 때와 같다. 지수함수를 적분하는 일이 매우 쉽기때문에 두 번째 치환이 훨씬 편하다. 이렇게 적분을 쉽게 해주는 치환을 생각하기 위해 아래와 같이 새로운 함수를 정의한다.
$$\sinh x=\frac{1}{2}(e^x -e^{-x}), \quad \cosh x =\frac{1}{2}(e^x +e^{-x})$$
이 함수가 쌍곡 함수인데 삼각함수와 매우 닮아서 이름도 비슷하게 붙였다. 하이퍼블릭 사인, 하이퍼볼릭 코사인으로 읽는다. 하이퍼볼릭 우리말로 쌍곡선 $x^2 -y^2 =1$을 매개화한 것으로 생각하면 된다. 그림을 참고하자.
쌍곡선 $x^2 -y^2 =1$과 $x$축 그리고 원점을 지나는 직선으로 둘러싸인 붉은색 영역 넓이가 $a/2$일 때, 직선과 쌍곡선이 만나는 점을 $(\cosh a, \sinh a)$로 정의한다. 이것은 원 $x^2+y^2 =1$과 $x$축 그리고 원점을 지나는 직선으로 둘러싸인 부채꼴 넓이가 $\theta/2$일 때 직선과 원이 만나는 점을 $(\cos\theta, \sin\theta)$로 정의하는 것과 같다. 더 자세하게 알고 싶다면 아래 연결고리를 열어 보자.
hyperbolic_Function.ggb
https://en.wikipedia.org/wiki/Hyperbolic_function
반응형
So you have finished reading the 쌍곡선 함수 적분 topic article, if you find this article useful, please share it. Thank you very much. See more: 역쌍곡선함수 적분, 쌍곡선함수 미분, Cosh 공식, Tanh 적분, 쌍곡함수, 삼각함수 적분, Sechx 적분, 쌍곡선함수 공식
