You are looking for information, articles, knowledge about the topic nail salons open on sunday near me filtre actif passe haut second ordre on Google, you do not find the information you need! Here are the best content compiled and compiled by the toplist.tfvp.org team, along with other related topics such as: filtre actif passe haut second ordre passe-haut ordre 2, exercice filtre passe-haut second ordre, filtre passe-haut, filtre passe-bas second ordre, filtre actif du second ordre exercice corrigé, filtre passe-haut pdf, filtre passe-bande, filtre second ordre
[su_youtube_advanced url=”https://www.youtube.com/watch?v=WOsERZoZOUQ”]
Les filtres du premier et du second ordre
- Article author: www.gecif.net
- Reviews from users: 29874
Ratings
- Top rated: 4.0
- Lowest rated: 1
- Summary of article content: Articles about Les filtres du premier et du second ordre La transmittance du filtre passe haut du premier ordre s’écrit alors : Calcul du module et de l’argument de la … …
- Most searched keywords: Whether you are looking for Les filtres du premier et du second ordre La transmittance du filtre passe haut du premier ordre s’écrit alors : Calcul du module et de l’argument de la …
- Table of Contents:

filtre actif passe haut second ordre
- Article author: issammabrouk.weebly.com
- Reviews from users: 7472
Ratings
- Top rated: 4.5
- Lowest rated: 1
- Summary of article content: Articles about filtre actif passe haut second ordre ou les transistors) de premier et de second ordre. … Les filtres passe-haut vont quant à eux laisser passer les hautes fréquences au dépend des basses. …
- Most searched keywords: Whether you are looking for filtre actif passe haut second ordre ou les transistors) de premier et de second ordre. … Les filtres passe-haut vont quant à eux laisser passer les hautes fréquences au dépend des basses.
- Table of Contents:

Filtre actif passe haut du 2ème ordre : schéma – Astuces Pratiques
- Article author: www.astuces-pratiques.fr
- Reviews from users: 44984
Ratings
- Top rated: 3.2
- Lowest rated: 1
- Summary of article content: Articles about Filtre actif passe haut du 2ème ordre : schéma – Astuces Pratiques Schéma du filtre actif passe haut d’ordre 2. Voici le schéma du filtre actif passe haut du deuxième ordre : schema filtre actif passe haut. Filtre actif passe … …
- Most searched keywords: Whether you are looking for Filtre actif passe haut du 2ème ordre : schéma – Astuces Pratiques Schéma du filtre actif passe haut d’ordre 2. Voici le schéma du filtre actif passe haut du deuxième ordre : schema filtre actif passe haut. Filtre actif passe … Avec un potentiomètre double, on peut réaliser un filtre actif passe haut avec réglage de la fréquence de coupure. Avec un ampli op, on obtient un filtre
- Table of Contents:
Schéma du filtre actif passe haut d’ordre 2
Réalisation d’un filtre actif d’ordre 2
Applications du filtre actif d’ordre 2
Filtre actif passe haut du 2ème ordre : schéma – Astuces Pratiques
- Article author: elearning-facsci.univ-annaba.dz
- Reviews from users: 1290
Ratings
- Top rated: 4.5
- Lowest rated: 1
- Summary of article content: Articles about Filtre actif passe haut du 2ème ordre : schéma – Astuces Pratiques Le filtre est donc un passe-haut du premier ordre. Les diagrammes de Bode sont tracés de la même manière que celui du passe-bas : Diagramme de Bode :. …
- Most searched keywords: Whether you are looking for Filtre actif passe haut du 2ème ordre : schéma – Astuces Pratiques Le filtre est donc un passe-haut du premier ordre. Les diagrammes de Bode sont tracés de la même manière que celui du passe-bas : Diagramme de Bode :. Avec un potentiomètre double, on peut réaliser un filtre actif passe haut avec réglage de la fréquence de coupure. Avec un ampli op, on obtient un filtre
- Table of Contents:
Schéma du filtre actif passe haut d’ordre 2
Réalisation d’un filtre actif d’ordre 2
Applications du filtre actif d’ordre 2

Filtre passe-haut — Wikipédia
- Article author: fr.wikipedia.org
- Reviews from users: 47357
Ratings
- Top rated: 3.1
- Lowest rated: 1
- Summary of article content: Articles about Filtre passe-haut — Wikipédia Un filtre passe-haut du premier ordre est … Une réalisation active et réalisation passive sont ici … …
- Most searched keywords: Whether you are looking for Filtre passe-haut — Wikipédia Un filtre passe-haut du premier ordre est … Une réalisation active et réalisation passive sont ici …
- Table of Contents:
Filtre idéal[modifier modifier le code]
Filtre passe-haut analogique[modifier modifier le code]
Voir aussi[modifier modifier le code]

Filtre passe-haut actif : 11 faits à connaître ! – Geeks Lambda
- Article author: fr.lambdageeks.com
- Reviews from users: 5632
Ratings
- Top rated: 3.9
- Lowest rated: 1
- Summary of article content: Articles about Filtre passe-haut actif : 11 faits à connaître ! – Geeks Lambda Les filtres de premier ordre sont la forme la plus simple de tous les filtres qui ne contiennent qu’un seul composant réactif, c’est-à-dire un condensateur, car … …
- Most searched keywords: Whether you are looking for Filtre passe-haut actif : 11 faits à connaître ! – Geeks Lambda Les filtres de premier ordre sont la forme la plus simple de tous les filtres qui ne contiennent qu’un seul composant réactif, c’est-à-dire un condensateur, car … Dans cet article, nous discuterons de quelques concepts de base liés au filtre passe-haut actif et tenterons de répondre à quelques questions dans les sections suivantes…
- Table of Contents:
Définition du filtre passe-haut actif
Quels sont les composants d’un filtre passe-haut actif
Schéma du circuit du filtre passe-haut actif
Principe de fonctionnement d’un filtre passe-haut actif
Réponse en temps et réponse en fréquence d’un HPF actif
Fonction de transfert de filtre passe-haut actif
Fréquence de coupure
Qu’entend-on par fréquence de coupure
Conception du filtre du filtre passe-haut actif
Filtre passe-haut actif de second ordre
Avantages de l’utilisation du filtre passe-haut actif
Application du filtre passe-haut actif
Foire aux Questions
À PROPOS

electronique.aop.free.fr
- Article author: electronique.aop.free.fr
- Reviews from users: 34829
Ratings
- Top rated: 4.0
- Lowest rated: 1
- Summary of article content: Articles about electronique.aop.free.fr La fonction de transfert obtenue correspond bien à celle d’un filtre passe-haut du deuxième ordre. Il vous reste maintenant à étudier l’évolution du module et … …
- Most searched keywords: Whether you are looking for electronique.aop.free.fr La fonction de transfert obtenue correspond bien à celle d’un filtre passe-haut du deuxième ordre. Il vous reste maintenant à étudier l’évolution du module et … Recueil de montages à amplificateur opérationnelelectronique ; electricite; EEA ; amplificateur operationnel ; AOP; ampliop; circuits ; montages; transistor; analogique ; numerique
- Table of Contents:

filtre actif passe haut second ordre
- Article author: philipperoux.nexgate.ch
- Reviews from users: 20098
Ratings
- Top rated: 4.2
- Lowest rated: 1
- Summary of article content: Articles about filtre actif passe haut second ordre Les filtres actifs de ce type obéissent à la même fonction de transfert. … filtre passe-haut du second ordre (L’A.O.P. A3 monté en suiveur de tension met … …
- Most searched keywords: Whether you are looking for filtre actif passe haut second ordre Les filtres actifs de ce type obéissent à la même fonction de transfert. … filtre passe-haut du second ordre (L’A.O.P. A3 monté en suiveur de tension met …
- Table of Contents:

See more articles in the same category here: Top 165 tips update new.
Les filtres du premier et du second ordre
Les filtres du premier et du second ordre
La fonction de transfert Vs/Ve des filtres, notée T, est appelée ici « la transmittance » du filtre, elle est donnée sous forme complexe, et n’est valable que dans les conditions suivantes :
la tension d’entrée Ve du filtre est un signal sinusoïdal
dans le cas des filtres passifs, le filtre est à vide (courant de sortie nul)
dans le cas des filtres actifs, les A.L.I. sont idéaux
Pour chaque filtre, un fichier au format ISIS Proteus 7.8 est disponible afin de simuler le comportement en fréquence du filtre dans ISIS Proteus 7.8 et d’obtenir le diagramme de Bode du filtre.
Animation interactive :
Voici une animation interactive qui vous permettra de bien comprendre le fonctionnement d’un filtre passe bas (cellule RC) et d’un filtre passe haut (cellule CR) du premier ordre .
Filtre passe bas : Filtre passe haut :
Pour télécharger cette animation (en un fichier .EXE fonctionnant sous Windows) afin de l’utiliser chez vous, cliquez ici.
Utilisation de cette animation :
la sinusoïde blanche représente la tension d’entrée du filtre : Ve
la sinusoïde verte est la tension de sortie du filtre à vide : Vs
pour faire varier la fréquence de Ve , baladez le curseur de votre souris sur la ligne rouge horizontale, entre Fréquence MIN et Fréquence MAX
vous pouvez changer de filtre en cliquant sur les boutons Passe bas et Passe haut
vous pouvez afficher seulement Ve en cliquant sur Cacher Vs
Remarque : lorsque vous déplacez le curseur de votre souris sur la ligne rouge horizontale, entre Fréquence MIN et Fréquence MAX, seule la fréquence de Ve varie. En effet, l’amplitude et la phase à l’origine de Ve restent constantes. Comme la phase à l’origine de Ve est nulle, le déphasage de Vs par rapport à Ve est égal à la phase à l’origine de Vs : il est appelé Phi sur l’animation, et est expimé en radian. Pour mettre à jour l’affichage de Phi, vous devez appuyer sur le bouton gauche de votre souris.
Pour le filtre passe bas, Phi est négatif et varie entre 0 et – pi/2 : Vs est en retard par rapport à Ve
Pour le filtre passe haut, Phi est positif et varie entre 0 et pi/2 : Vs est en avance par rapport à Ve
Voici les équations de Ve et de Vs :
: amplitude unitaire constante et phase à l’origine nulle
: A (l’amplitude) et Phi (la phase à l’origine) varient en fonction de la fréquence de Ve
Filtre passe bas passif du premier ordre (ou cellule RC) :
Diagramme de Bode (en vert le gain et en rouge la phase) :
Télécharger le fichier ISIS Proteus de ce filtre avec son diagramme de Bode
Nous supposons que le filtre est à vide. Ve est la tension sinusoïdale d’entrée, et Vs est la tension sinusoïdale de sortie.
La phase à l’origine de Ve est nulle, et son amplitude maximale est unitaire :
L’amplitude maximale de Vs est notée A, et sa phase à l’origine est notée Phi :
Calcul de Vs en fonction de Ve :
Comme le filtre est à vide (le courant de sortie est nul), on peut appliquer le pont diviseur de tension pour calculer Vs en fonction de Ve. Le pont diviseur nous donne :
La transmittance (notée T complexe) est le rapport Vs / Ve :
On en déduit que :
Sachant que l’impédance de la résistance vaut :
Et que l’impédance du condensateur vaut :
On en déduit que la transmittance du filtre passe bas est :
Et en multipliant le numérateur et le dénominateur par on obtient :
Appelons oméga zéro le rapport 1/RC :
La transmittance du filtre passe bas du premier ordre s’écrit alors :
Calcul du module et de l’argument de la transmittance complexe:
Le module de la transmittance complexe est :
Et son argument est :
Faisons tendre oméga vers zéro et vers l’infini :
Comportement du filtre en basse fréquence (lorsque oméga tend vers zéro) :
On en déduit que :
Comportement du filtre en haute fréquence (lorsque oméga tend vers l’infini) :
On en déduit que :
Le module de la transmittance varie donc entre 0 et 1, et l’argument de la transmittance varie entre -Pi/2 et 0, en fonction de la fréquence :
Vous pouvez tester expérimentalement ces intervales de valeur en faisant varier la fréquence sur l’animation qui est en haut de cette page.
Filtre passe haut passif du premier ordre (ou cellule CR) :
Diagramme de Bode (en vert le gain et en rouge la phase) :
Télécharger le fichier ISIS Proteus de ce filtre avec son diagramme de Bode
Calcul de Vs en fonction de Ve :
Comme le filtre est à vide (le courant de sortie est nul), on peut appliquer le pont diviseur de tension pour calculer Vs en fonction de Ve. Le pont diviseur nous donne :
La transmittance (notée T complexe) est le rapport Vs / Ve :
On en déduit que :
Sachant que l’impédance de la résistance vaut :
Et que l’impédance du condensateur vaut :
On en déduit que la transmittance du filtre passe haut est :
Et en divisant le numérateur et le dénominateur par R on obtient :
Appelons oméga zéro le rapport 1/RC :
La transmittance du filtre passe haut du premier ordre s’écrit alors :
Calcul du module et de l’argument de la transmittance complexe:
Le module de la transmittance complexe est :
Et son argument est :
Faisons tendre oméga vers zéro et vers l’infini :
Comportement du filtre en basse fréquence (lorsque oméga tend vers zéro) :
On en déduit que :
Comportement du filtre en haute fréquence (lorsque oméga tend vers l’infini) :
On en déduit que :
Le module de la transmittance varie donc entre 0 et 1, et l’argument de la transmittance varie entre 0 et Pi/2, en fonction de la fréquence :
Vous pouvez tester expérimentalement ces intervales de valeur en faisant varier la fréquence sur l’animation qui est en haut de cette page.
Les filtres actifs du premier ordre :
Chaque filtre est un quadripôle avec :
Ve = potentiel du point E par rapport à la masse = la tension d’entrée
= potentiel du point par rapport à la masse = la tension d’entrée Vs = potentiel du point S par rapport à la masse = la tension de sortie
= potentiel du point par rapport à la masse = la tension de sortie Vs/Ve = la transmittance T du filtre
Le filtre passe bas
Sa structure électronique à base d’A.L.I. est :
Diagramme de Bode (en vert le gain et en rouge la phase) :
Télécharger le fichier ISIS Proteus de ce filtre avec son diagramme de Bode
Sa transmittance complexe est :
Avec la pulsation ω 0 qui vaut :
Le filtre passe haut
Sa structure électronique à base d’A.L.I. est :
Diagramme de Bode (en vert le gain et en rouge la phase) :
Télécharger le fichier ISIS Proteus de ce filtre avec son diagramme de Bode
Sa transmittance complexe est :
Avec la pulsation ω 0 qui vaut :
Le filtre passe bande
Sa structure électronique à base d’A.L.I. est :
Diagramme de Bode (en vert le gain et en rouge la phase) :
Télécharger le fichier ISIS Proteus de ce filtre avec son diagramme de Bode
Sa transmittance complexe est :
Avec la pulsation ω 0 qui vaut :
Le filtre coupe bande
Sa structure électronique à base d’A.L.I. est :
Diagramme de Bode (en vert le gain et en rouge la phase) :
Télécharger le fichier ISIS Proteus de ce filtre avec son diagramme de Bode
Sa transmittance complexe est :
Avec :
Les filtres passe tout (ou circuits déphaseurs)
La particularité des filtres passe tout est que quelque soit la fréquence du signal d’entrée Ve le module de la transmittance complexe sera toujours égal à 1. Si la fréquence de Ve varie, seul le déphasage entre Ve et Vs varie, d’o&; le nom de “circuits déphaseurs” :
Circuit déphaseur à avance de phase :
Diagramme de Bode (en vert le gain et en rouge la phase) :
Télécharger le fichier ISIS Proteus de ce filtre avec son diagramme de Bode
Sa transmittance complexe est :
Circuit déphaseur à retard de phase :
Diagramme de Bode (en vert le gain et en rouge la phase) :
Télécharger le fichier ISIS Proteus de ce filtre avec son diagramme de Bode
Sa transmittance complexe est :
Transmittances des filtres du second ordre :
Dans les 5 transmittances complexes ci-dessous le dénominateur est identique. La grandeur z est le coefficient d’amortissement du filtre (indique si le filtre est résonnant ou non), et 2.z est l’inverse du facteur de qualité Q du filtre :
z = le coefficient d’amortissement 2.z=1/Q Q = le facteur de qualité
Remarque : z et Q sont des grandeurs sans unité.
Transmittance du filtre passe bas du second ordre :
Transmittance du filtre passe haut du second ordre :
Transmittance du filtre passe bande du second ordre :
Transmittance du filtre coupe bande du second ordre :
Transmittance du filtre passe tout du second ordre :
Structures électroniques des filtres passifs du second ordre :
Chaque filtre est un quadripôle avec :
Ve = potentiel du point E par rapport à la masse = la tension d’entrée
= potentiel du point par rapport à la masse = la tension d’entrée Vs = potentiel du point S par rapport à la masse = la tension de sortie
= potentiel du point par rapport à la masse = la tension de sortie Vs/Ve = la transmittance T du filtre
Remarque : dans tous les cas ci-dessous on a :
Filtre passe bas du second ordre (2 cellules RC en cascade) :
Diagramme de Bode (en vert le gain et en rouge la phase) :
Télécharger le fichier ISIS Proteus de ce filtre avec son diagramme de Bode
Transmittance des 2 cellules RC en cascade dans le cas o&; C1=C2=C et R1=R2=R :
Filtre passe haut du second ordre (2 cellules CR en cascade) :
Diagramme de Bode (en vert le gain et en rouge la phase) :
Télécharger le fichier ISIS Proteus de ce filtre avec son diagramme de Bode
Filtre passe bas du troisième ordre (3 cellules RC en cascade) :
Diagramme de Bode (en vert le gain et en rouge la phase) :
Télécharger le fichier ISIS Proteus de ce filtre avec son diagramme de Bode
Filtre passe haut du troisième ordre (3 cellules CR en cascade, appelé aussi réseau déphaseur) :
Diagramme de Bode (en vert le gain et en rouge la phase) :
Télécharger le fichier ISIS Proteus de ce filtre avec son diagramme de Bode
Transmittance du réseau déphaseur dans le cas o&; C1=C2=C3=C et R1=R2=R3=R :
Rappel :
Filtre passe bande (appelé aussi pont de Wien) :
Diagramme de Bode (en vert le gain et en rouge la phase) :
Télécharger le fichier ISIS Proteus de ce filtre avec son diagramme de Bode
Transmittance du pont de Wien dans le cas o&; C1=C2=C et R1=R2=R :
A vide, le pont de Wien est équivalent aux deux filtres suivants :
Filtre passe bande (cellule CR suivie d’une cellule RC, équivalent à vide au pont de Wien) :
Filtre passe bande (cellule RC suivie d’une cellule CR, équivalent à vide au pont de Wien) :
Filtre coupe bande (réjecteur de bande) :
Diagramme de Bode (en vert le gain et en rouge la phase) :
Télécharger le fichier ISIS Proteus de ce filtre avec son diagramme de Bode
Transmittance dans le cas o&; C1=C2=C, R1=2.R et R2=R/2 :
Filtre coupe bande (réjecteur de bande) :
Diagramme de Bode (en vert le gain et en rouge la phase) :
Télécharger le fichier ISIS Proteus de ce filtre avec son diagramme de Bode
Transmittance dans le cas o&; C1=C2=C et R1=R2=R :
Filtre sélectif (structure en double T) :
Diagramme de Bode (en vert le gain et en rouge la phase) :
Télécharger le fichier ISIS Proteus de ce filtre avec son diagramme de Bode
Transmittance du filtre en double T dans le cas o&; :
R1=R2=R
C1=C2=C
C3=2.C
R3=R/2
Rappel :
Les filtres actifs du second ordre :
La structure de Rauch
La structure de Rauch est un montage électronique utilisant 5 dipôles d’admittance Y1 à Y5 (résistances ou condensateurs) autour d’un A.L.I. :
◊ si un dipôle est une résistance R son admittance est Y=1/R ◊ si un dipôle est un condensateur C son admittance complexe est Y=j.C.ω
Structure de Rauch
Dans le cas général, la transmittance de la structure de Rauch en fonction des 5 admittances Y1 à Y5 est la suivante :
Remarque : étant donné qu’il y a un seul terme au numérateur de la transmittance, la structure de Rauch permet de faire seulement des filtres passe bas, passe haut et passe bande. Les filtres coupe bande (2 termes au numérateur) et passe tout (3 termes au numérateur) ne sont pas réalisables avec la structure de Rauch.
Filtre passe bas à structure de Rauch
Sa structure électronique à base d’A.L.I. est :
Diagramme de Bode (en vert le gain et en rouge la phase) :
Télécharger le fichier ISIS Proteus de ce filtre avec son diagramme de Bode
Sa transmittance complexe est obtenue avec :
Y1=Y3=Y4=1/R Y2=j.C2.ω Y5=j.C1.ω
La forme générale de la transmittance complexe du filtre passe bas du second ordre est :
Avec dans le cas particulier de la structure de Rauch :
Filtre passe haut à structure de Rauch
Sa structure électronique à base d’A.L.I. est :
Diagramme de Bode (en vert le gain et en rouge la phase) :
Télécharger le fichier ISIS Proteus de ce filtre avec son diagramme de Bode
Sa transmittance complexe est obtenue avec :
Y1=Y3=Y4=j.C.ω Y2=1/R2 Y5=1/R1
La forme générale de la transmittance complexe du filtre passe haut du second ordre est :
Avec dans le cas particulier de la structure de Rauch :
Filtre passe bande à structure de Rauch
Sa structure électronique à base d’A.L.I. est :
Diagramme de Bode (en vert le gain et en rouge la phase) :
Télécharger le fichier ISIS Proteus de ce filtre avec son diagramme de Bode
Sa transmittance complexe est obtenue avec :
Y3=Y4=j.C.ω Y1=1/R1 Y2=1/R2 Y5=1/R3
La forme générale de la transmittance complexe du filtre passe bande du second ordre est :
Avec dans le cas particulier de la structure de Rauch :
Remarque : Δω est la largeur de la bande passante à -3 dB.
Dans le cas du filtre passe bande, le facteur de qualité Q est :
La structure de Sallen & Key
La structure de Sallen & Key est un montage électronique utilisant 4 dipôles d’impédance Z1 à Z4 (résistances ou condensateurs) autour d’un A.L.I. branché en suiveur :
◊ si un dipôle est une résistance R son impédance est Z=R ◊ si un dipôle est un condensateur C son impédance complexe est Z=1/(j.C.ω)
Structure de Sallen & Key
Remarque : le montage suiveur à A.L.I. peut être remplacé par un amplificateur non inverseur.
Filtre passe bas à structure de Sallen & Key
Sa structure électronique à base d’A.L.I. branché en montage suiveur est :
Diagramme de Bode (en vert le gain et en rouge la phase) :
Télécharger le fichier ISIS Proteus de ce filtre avec son diagramme de Bode
Sa transmittance complexe est :
On en déduit que pour ce filtre on a :
Remarque : comme le coefficient d’amortissement z est unitaire, le dénominateur de la transmittance est le carré d’une somme et peut alors se factoriser ainsi :
Filtre passe haut à structure de Sallen & Key
Sa structure électronique à base d’A.L.I. branché en montage suiveur est :
Diagramme de Bode (en vert le gain et en rouge la phase) :
Télécharger le fichier ISIS Proteus de ce filtre avec son diagramme de Bode
Sa transmittance complexe est :
On en déduit que pour ce filtre on a :
Remarque : comme le coefficient d’amortissement z est unitaire, le dénominateur de la transmittance est le carré d’une somme et peut alors se factoriser ainsi :
Filtres légèrement résonnant pouvant servir de passe bande
Les deux filtres actifs suivants sont obtenus avec 2 cellules RC associées à un A.L.I. branché en suiveur. Bien que leur montage électronique soit similaire à la structure de Sallen & Key, ces filtres présentent comme différence essentielle une réponse en fréquence légèrement résonnante sur le diagramme de Bode. Ces filtres peuvent alors servir dans certains cas de filtres passe bande.
Filtre passe bas légèrement résonnant
Sa structure électronique à base d’A.L.I. branché en montage suiveur est :
Diagramme de Bode (en vert le gain et en rouge la phase) :
Télécharger le fichier ISIS Proteus de ce filtre avec son diagramme de Bode
Sa transmittance complexe est :
Avec :
On peut remarquer que le coefficient d’amortissement de ce filtre est unitaire : z=1
Remarque : vu la forme de sa transmittance (avec ses 2 termes au numérateur), ce filtre n’est ni un filtre passe bas du second ordre, ni un filtre passe haut du second ordre, ni un filtre passe bande du second ordre. En fait, on peut remarquer que la transmittance de ce filtre est la somme de deux transmittances :
◊ la transmittance d’un filtre passe bas de second ordre (d’o&; le terme de degré 0 au numérateur) ◊ la transmittance d’un filtre passe bande de second ordre (d’o&; le terme de degré 1 au numérateur)
Filtre passe haut légèrement résonnant
Sa structure électronique à base d’A.L.I. branché en montage suiveur est :
Diagramme de Bode (en vert le gain et en rouge la phase) :
Télécharger le fichier ISIS Proteus de ce filtre avec son diagramme de Bode
Sa transmittance complexe est :
Avec :
On peut remarquer que le coefficient d’amortissement de ce filtre est unitaire : z=1
Remarque : vu la forme de sa transmittance (avec ses 2 termes au numérateur), ce filtre n’est ni un filtre passe bas du second ordre, ni un filtre passe haut du second ordre, ni un filtre passe bande du second ordre. En fait, on peut remarquer que la transmittance de ce filtre est la somme de deux transmittances :
◊ la transmittance d’un filtre passe haut de second ordre (d’o&; le terme de degré 2 au numérateur) ◊ la transmittance d’un filtre passe bande de second ordre (d’o&; le terme de degré 1 au numérateur)
Exemple d’activité pédagogique autour des filtres :
Le TP suivant permet d’expérimenter la fonction filtrage dans ISIS Proteus :
Modélisation et simulation_Fonction filtrage.doc
Et voici les fichiers ISIS Proteus utilisés dans le TP :
Modulation par sommateur 2 signaux_eleve.DSN
Modulation par sommateur 2 signaux_PROF2.DSN
sommation de 3 signaux2 filtres 2eme ordre passebande eleve .DSN
Filtre actif passe haut du 2ème ordre : schéma
Avec un potentiomètre double, on peut réaliser un filtre actif passe haut avec réglage de la fréquence de coupure. Avec un ampli op, on obtient un filtre actif d’ordre 2 qui permet une atténuation bien prononcée des basses (pente de 12dB par octave). Voici donc le schéma du filtre actif, comment brancher le potentiomètre de réglage de la fréquence et quelques explications sur la conception de ce petit schéma.
Schéma du filtre actif passe haut d’ordre 2
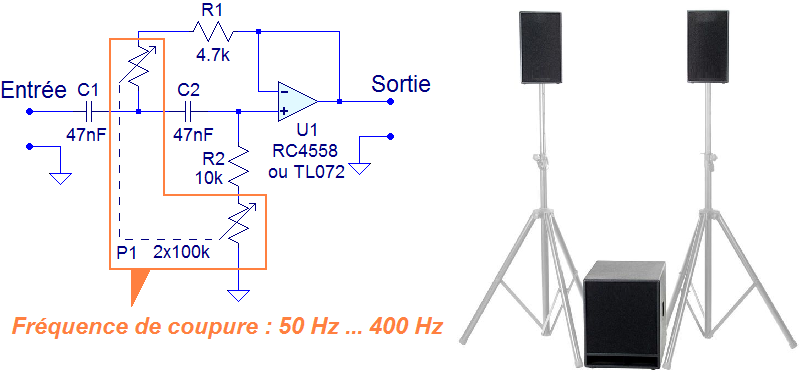
Voici le schéma du filtre actif passe haut du deuxième ordre :
Filtre actif passe haut d’ordre 2 : le schéma
Le filtre actif passe haut repose sur un ampli op utilisé dans une structure de Sallen-Key. La structure de Sallen-Key ne nécessite que 4 composants autour de l’ampli op. C’est pour cela qu’elle a été choisie. Comme les condensateurs ont des valeurs fixes, l’élément variable est donc nécessairement la résistance (ici, le potentiomètre).
C1 et C2 sont choisies de valeur identique entre elles pour la simplicité des calculs. Le potentiomètre doit être doublé (stéréo) pour avoir deux résistances variables couplées (qui valent la même valeur et varient de la même façon quand on tourne l’axe du potentiomètre). L’amortissement du filtre actif de Sallen-Key est alors défini uniquement par le rapport des résistances (potentiomètre + R1 pour l’une, potentiomètre + R2 pour l’autre). R2 est choisie supérieure à R1 pour obtenir une réponse en fréquence de type Butterworth (le meilleur compromis souvent adopté en audio) lorsque le potentiomètre est en butée (valeur nulle, fréquence de coupure du filtre la plus élevée). Lorsque le potentiomètre augmente en valeur, le rapport des deux résistances totales tend vers 1 et la réponse en fréquence devient alors un peu plus arrondie autour de la fréquence de coupure.
Mathématiquement parlant, l’amortissement du filtre est égal à la racine carrée du rapport des résistances totales. Lorsque le potentiomètre est en butée, il vaut racine de (4.7k/10k), soit environ 0.7 (filtre de Butterworth) et lorsque la fréquence de coupure baisse (la valeur du potentiomètre augmente, l’amortissement se rapproche de 1. La réponse en fréquence est alors plus arrondie autour de la fréquence de coupure (la réponse en fréquence va moins “dans le coin”, à la façon des poneys paresseux dans les manèges qui ne vont pas suffisamment dans les coins !).
Voici les réponses en fréquence du filtre actif simulées avec LTSpice IV :
Filtre actif passe haut d’ordre 2 : la réponse en fréquence
La fréquence de coupure va de 48Hz à 480Hz environ.
Montage du potentiomètre stéréo double pour le filtre actif
Si on souhaite que la fréquence de coupure la plus basse se situe en butée du côté gauche (comme un ampli au volume minimum), il faut brancher le potentiomètre double de cette façon vers le filtre actif passe haut :
Filtre actif passe haut du 2ème ordre : potentiomètre de réglage de la fréquence
Réalisation d’un filtre actif d’ordre 2
Pour établir la liaison entre le potentiomètre de réglage de fréquence (monté en face avant de votre réalisation par exemple) et le filtre actif, on peut utiliser un câble blindé à 3 fils. En effet, une des quatre connexions correspond à la masse. Cette liaison de masse entre le filtre et le potentiomètre permet de blinder les trois autres fils qui portent le signal audio. Voici un exemple de câblage pour une version stéréo de ce filtre actif.Branchement du potentiomètre 2 x 100kOhms de réglage de fréquence :
Branchement du potentiomètre 2 x 100kOhms de réglage de fréquence
Applications du filtre actif d’ordre 2
Ce filtre actif est tout à fait adapté à un système 2.1 avec caisson de grave et satellites. Chaque satellite devra avoir son filtre actif. Il n’est pas possible avec cette méthode de faire un réglage de fréquence commun aux deux satellites (stéréo) étant donné qu’on trouve difficilement des potentiomètres quadruples (4 résistances qui varient simultanément).
Exemple de réalisation de deux filtres actifs passe haut sur une maquette d’ampli classe D :
Ici, il s’agit d’un ampli classe D stéréo 2 x 250W, alimenté par une alimentation à découpage (demi pont basé sur un transfo d’alimentation de PC ATX et d’un driver IR2153D). Les filtres actifs sont basés sur un TL072 et deux potentiomètres doubles 2 x 100kOhms. On voit les deux réglages de fréquences et le potentiomètre de volume stéréo, ainsi que le connecteur RCA d’entrée et le bornier haut-parleur (sortie de l’ampli).
Filtre passe-haut — Wikipédia
Image sur laquelle a été appliqué un filtre passe-haut (résultat à droite)
Un filtre passe-haut (en anglais, high-pass filter ou HPF) est un filtre qui laisse passer les hautes fréquences et qui atténue les basses fréquences, c’est-à-dire les fréquences inférieures à la fréquence de coupure. Il pourrait également être appelé filtre coupe-bas. Le filtre passe-haut est l’inverse du filtre passe-bas et ces deux filtres combinés forment un filtre passe-bande.
Le concept de filtre passe-haut est une transformation mathématique appliquée à des données (un signal). L’implémentation d’un filtre passe-haut peut se faire numériquement ou avec des composantes électroniques. Cette transformation a pour fonction d’atténuer les fréquences inférieures à sa fréquence de coupure f c {\displaystyle f_{c}} et ce, dans le but de conserver uniquement les hautes fréquences. La fréquence de coupure du filtre est la fréquence séparant les deux modes de fonctionnement idéaux du filtre : bloquant ou passant.
Le filtre idéal est le filtre théorique capable de modifier de façon immédiate son gain (de 1 à 0 ou de 0 à 1, en échelle linéaire) à sa fréquence dite de coupure. Dans la réalité, un filtre possède sa fréquence de coupure au gain Gmax -3 dB et avant ce gain croît de n × 20 d B {\displaystyle n\times 20dB} par décade (filtre d’ordre n {\displaystyle n} ).
Un filtre passe-haut peut être implémenté de façon analogique avec des composantes électroniques. Par conséquent, ce genre de filtre s’applique sur des signaux continus en temps réel. Les composantes et la configuration du circuit fixeront les différentes caractéristiques du filtre, telles que l’ordre, la fréquence de coupure et son diagramme de Bode. Les filtres analogiques classiques sont du premier ou du second ordre. Il existe plusieurs familles de filtres analogiques : Butterworth, Tchebychev, Bessel, elliptique, etc. L’implémentation des filtres de même famille se fait généralement en utilisant la même configuration de circuit, et ceux-ci possèdent la même forme de fonction de transfert, mais ce sont les paramètres de celle-ci qui changent, donc la valeur des composantes du circuit électrique.
Filtre passe-haut du premier ordre [ modifier | modifier le code ]
Un filtre passe-haut du premier ordre est caractérisé par sa fréquence de coupure f c {\displaystyle f_{c}} et par son gain dans la bande-passante K {\displaystyle K} . La fonction de transfert du filtre est obtenue en dénormalisant le filtre passe-haut normalisé en remplaçant ω n {\displaystyle \omega _{n}} par ω c / ω {\displaystyle \omega _{c}/\omega } ce qui donne la fonction de transfert suivante :
H ( j ω ) = v o v i = K j ω ω c 1 + j ω ω c {\displaystyle H(j\omega )={\frac {v_{o}}{v_{i}}}={\frac {Kj{\frac {\omega }{\omega _{c}}}}{1+j{\frac {\omega }{\omega _{c}}}}}}
où
ω = 2 π f {\displaystyle \omega =2\pi f}
ω c = 2 π f c {\displaystyle \omega _{c}=2\pi f_{c}}
Le module et la phase de la fonction de transfert sont égaux à :
| H ( ω ) | = | v o v i | = K ω ω c > 1 + > ( ω ω c ) 2 > > {\displaystyle |H(\omega )|=\left|{\frac {v_{o}}{v_{i}}}\right|={\frac {K{\frac {\omega }{\omega _{c}}}}{\sqrt {1+\left({\frac {\omega }{\omega _{c}}}\right)^{2}}}}}
ϕ ( ω ) = arg H ( j ω ) = π 2 − arg ( 1 + j ω ω c ) = π 2 − arctan ( ω ω c ) {\displaystyle \phi (\omega )=\arg H(j\omega )={\frac {\pi }{2}}-\arg \left(1+j{\frac {\omega }{\omega _{c}}}\right)={\frac {\pi }{2}}-\arctan \left({\frac {\omega }{\omega _{c}}}\right)}
Il y a plusieurs méthodes pour implémenter ce filtre. Une réalisation active et réalisation passive sont ici présentées. K est le gain du filtre.
Schéma d’un filtre passe-haut
La manière la plus simple de réaliser physiquement ce filtre est d’utiliser un circuit RC. Comme son nom l’indique, ce circuit est constitué d’un condensateur de capacité C {\displaystyle C} et d’une résistance R {\displaystyle R} . Ces deux éléments sont placés en série avec la source v i {\displaystyle v_{i}} du signal. Le signal de sortie v o {\displaystyle v_{o}} est récupéré aux bornes de la résistance. Le circuit est identique à celui du filtre passe-bas mais les positions de la résistance et du condensateur sont inversées. Pour retrouver la fonction de transfert de ce filtre, il faut travailler dans le domaine de Laplace en utilisant les impédances des éléments. Avec cette technique, le circuit devient un simple diviseur de tension, et on obtient :
H ( j ω ) = v o v i = j R C ω 1 + j R C ω {\displaystyle H(j\omega )={\frac {v_{o}}{v_{i}}}={\frac {jRC\omega }{1+jRC\omega }}}
Dans cette équation, j {\displaystyle j} est un nombre complexe, tel que j² = -1, et ω {\displaystyle \omega } est la pulsation du circuit ou fréquence radiale, exprimée en rad/s. Comme la fréquence de coupure d’un circuit RC est :
f c = 1 2 π R C {\displaystyle f_{c}={\frac {1}{2\pi RC}}} ω c = 1 R C {\displaystyle \omega _{c}={\frac {1}{RC}}}
Ici ω c {\displaystyle \omega _{c}} , la pulsation de coupure, est également la pulsation propre ω o {\displaystyle \omega _{o}} du circuit, elle est également l’inverse de la constante de temps τ {\displaystyle \tau } du circuit. Ainsi, on obtient bel et bien la fonction de transfert typique du filtre passe-haut du premier ordre.
On retrouve avec les grandeurs physiques observables utilisées dans les diagrammes de Bode :
1er ordre) Diagramme de Bode d’un filtre passe haut (système duordre)
Le gain en décibels :
G d B ( ω ) = 20 ⋅ log | H ( j ω ) | = 20 ⋅ log ( ω ω c ) − 10 ⋅ log ( 1 + > ( ω ω c ) 2 > ) {\displaystyle G_{dB}(\omega )=20\cdot \log |H(j\omega )|=20\cdot \log \left({\frac {\omega }{\omega _{c}}}\right)-10\cdot \log \left(1+{\left({\frac {\omega }{\omega _{c}}}\right)}^{2}\right)}
La phase en radians :
ϕ ( ω ) = arg H ( ω ) = π 2 − arg ( 1 + j ω ω c ) {\displaystyle \phi (\omega )=\arg H(\omega )={\frac {\pi }{2}}-\arg \left(1+j{\frac {\omega }{\omega _{c}}}\right)}
= π 2 − arctan ( ω ω c ) {\displaystyle ={\frac {\pi }{2}}-\arctan \left({\frac {\omega }{\omega _{c}}}\right)}
On distingue alors deux situations idéales :
Lorsque ω ≪ ω c {\displaystyle \omega \ll \omega _{c}}
G d B ∼ 20 ⋅ log ( ω ω c ) {\displaystyle G_{dB}\sim 20\cdot \log \left({\frac {\omega }{\omega _{c}}}\right)} ϕ ≃ 90 {\displaystyle \phi \simeq 90}
Lorsque ω ≫ ω c {\displaystyle \omega \gg \omega _{c}}
G d B ≃ 0 {\displaystyle G_{dB}\simeq 0} ϕ ≃ 0 {\displaystyle \phi \simeq 0}
On remarque que pour ω = ω c {\displaystyle \omega =\omega _{c}} , on a G d B {\displaystyle G_{dB}} = -3 dB.
Filtre du second ordre [ modifier | modifier le code ]
Un filtre passe-haut du second ordre est caractérisé par sa fréquence propre f o {\displaystyle f_{o}} et par le facteur de qualité Q. Il est représenté par la fonction de transfert suivante :
H ( j ω ) = v o v i = − K ( ω ω 0 > ) 2 > 1 − ( ω ω 0 > ) 2 > + j ( ω ω 0 ) Q {\displaystyle H(j\omega )={\frac {v_{o}}{v_{i}}}={\frac {-K({\frac {\omega }{\omega _{0}}})^{2}}{1-({\frac {\omega }{\omega _{0}}})^{2}+j{\frac {({\frac {\omega }{\omega _{0}}})}{Q}}}}}
où
ω = 2 π f > {\displaystyle \omega =2\pi f\,}
ω o = 2 π f o > {\displaystyle \omega _{o}=2\pi f_{o}\,}
Le module de la fonction de transfert est donc égal à :
| H ( ω ) | = | v o v i | = | K | ( ω ω 0 > ) 2 > > ( 1 − ( ω ω 0 > ) 2 > > ) 2 > + ( ω ω 0 Q > ) 2 > > {\displaystyle |H(\omega )|={\biggl |}{\frac {v_{o}}{v_{i}}}{\biggr |}={\frac {|K|{\Bigl (}{\frac {\omega }{\omega _{0}}}{\Bigr )}^{2}}{\sqrt {{\Bigl (}1-({\frac {\omega }{\omega _{0}}})^{2}{\Bigr )}^{2}+{\Biggl (}{\frac {\frac {\omega }{\omega _{0}}}{Q}}{\Biggr )}^{2}}}}}
La manière la plus simple de réaliser physiquement ce filtre est d’utiliser un circuit RLC. Comme son nom l’indique, ce circuit est constitué d’une résistance R {\displaystyle R} , d’un condensateur de capacité C {\displaystyle C} et d’une bobine d’inductance L {\displaystyle L} . Ces trois éléments sont placés en série avec la source v i {\displaystyle v_{i}} du signal. Le signal de sortie v o {\displaystyle v_{o}} est récupéré aux bornes de la bobine. Pour retrouver la fonction de transfert de ce filtre, il faut travailler dans le domaine de Laplace en utilisant les impédances des éléments. Avec cette technique, le circuit devient un simple diviseur de tension, et on obtient :
H ( j ω ) = v o v i = − L C > ω 2 > 1 + j R C ω − L C > ω 2 > {\displaystyle H(j\omega )={\frac {v_{o}}{v_{i}}}={\frac {-LC\omega ^{2}}{1+jRC\omega -LC\omega ^{2}}}}
Avec :
ω o = 1 > L C > {\displaystyle \omega _{o}={\frac {1}{\sqrt {LC}}}}
Q = 1 R > L C > {\displaystyle Q={\frac {1}{R}}{\sqrt {\frac {L}{C}}}}
Le module de ce circuit est :
| H ( ω ) | = | v o v i | = | K | L C > ω 2 > > > R 2 > > C 2 > > ω 2 > + ( 1 − L C > ω 2 > > ) 2 > > {\displaystyle |H(\omega )|={\biggl |}{\frac {v_{o}}{v_{i}}}{\biggr |}={\frac {|K|LC\omega ^{2}}{\sqrt {R^{2}C^{2}{\omega }^{2}+{\big (}1-LC{\omega }^{2})^{2}}}}}
Sur les autres projets Wikimedia :
So you have finished reading the filtre actif passe haut second ordre topic article, if you find this article useful, please share it. Thank you very much. See more: passe-haut ordre 2, exercice filtre passe-haut second ordre, filtre passe-haut, filtre passe-bas second ordre, filtre actif du second ordre exercice corrigé, filtre passe-haut pdf, filtre passe-bande, filtre second ordre
